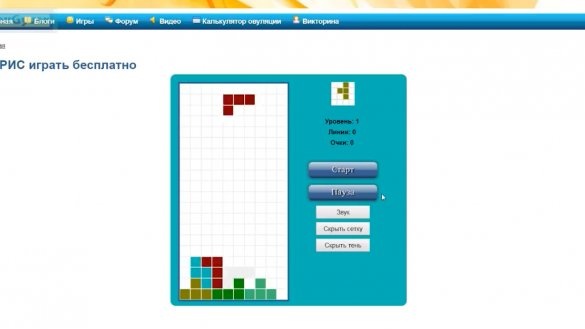
Avui estudiarem els elements del joc Tetris escrits sota la plataforma arduino i matriu LED.
L’autor d’aquest producte casolà és AlexGyver, l’autor del canal YouTube del mateix nom. Benvingut al meravellós món dels píxels quadrats.
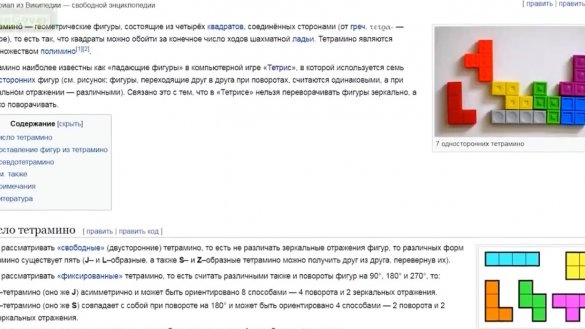
Comencem amb la història. El Tetris és un joc en què les figures formades per 4 quadrats cauen de dalt a baix. En diferents combinacions, aquestes formes es poden girar i moure cap a l'esquerra ia la dreta. L’objectiu del joc és recollir nivells horitzontals que s’esborren i s’atorguen punts. Perdre es considera el moment en què la nova figura no ha de caure enlloc. Tetris va ser inventat pel programador soviètic Alexei Leonidovich Pazhitnov.
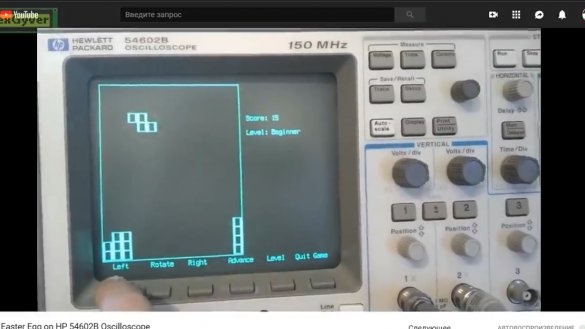
La versió original de Pascal va aparèixer el 6 de juny de 1984. Des d’aleshores, Tetris ha recorregut un llarg recorregut i s’ha portat a totes les plataformes en què generalment és possible jugar a jocs, així com a dispositius no destinats a jocs, com per exemple, com una calculadora d’enginyeria, un osciloscopi i, no s’ho creu, una soldadura.
Pel nombre de versions comercials venudes, Tetris és superior a qualsevol altre joc de la història de la humanitat. Per només un Game Boy, es van vendre 35 milions d’exemplars, sense oblidar-nos del portàtil Brick Game, que gairebé tots tenien alhora.
Començarem la implementació de tetris a arduino i una matriu de colors amb l’anàlisi de “muletes”. La matriu consisteix en leds de tres adreces de tres colors. El problema d’aquest tipus de matrius és que és massa genial. El color de cada píxel està codificat amb 24 bits, és a dir, 8 bits per a cada component: vermell, verd i blau. No hi ha cap tipus de dades sobre arduino, hi ha les següents: 32 bits.
Els colors de tots els LED s’han de guardar a la memòria RAM, ja que els canviarem. I a més, per a una matriu de 16 per 16, tenim exactament 1 KB de memòria dinàmica ocupada, i arduo nano en té només 2.
Afegiu unes quantes biblioteques més i comenceu a escriure codi, la memòria s’acabarà. L’autor bàsicament no utilitza, per exemple, arduino mega, on hi ha més memòria. L’objectiu és convertir el joc en arduino nano, utilitzant eines simples, estàndard i conegudes, però al mateix temps enfocaments i “muletes” no estàndard i amb la seva ajuda aconseguir el codi més òptim.
La primera "crossa" serà la negativa a emmagatzemar per separat a la memòria les posicions de les figures i, en general, tot el que passi a la pantalla.Hem d’emmagatzemar les coordenades dels punts de la figura d’alimentació i les coordenades dels punts de les figures ja caigudes, és a dir, com a màxim, necessitem un altre 1 array, bidimensional 16 per 16, i això és de fins a 256 bytes.
Vostè i jo ja tenim una gamma de colors per a tots els píxels, utilitzem-ho. De fet, a més que podem posar un punt de color a la matriu, podem mesurar la llum d’un punt existent de manera que treballem amb colors.
Tetris comença amb un bloc que cau, que està controlat per botons i té 2 coordenades al sistema de coordenades de la matriu. És molt senzill, construïm un temporitzador segons el qual caurà el bloc. Aquesta és la biblioteca de l’autor que podeu llegir al lloc.
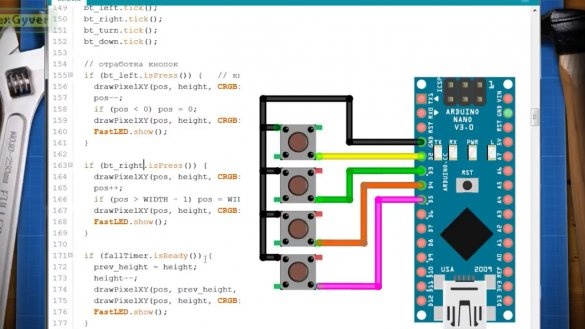
Per processar botons, l’autor també utilitza la seva biblioteca. L’esquema de connexió dels botons és ridículament senzill: 4 botons, 8 fils.
A cada pas del temporitzador, dibuixem un punt un píxel per sota de l’antic i dibuixem l’antic punt en negre, és a dir, apaguem el LED. Fent clic al botó, fem el mateix, però amb una coordenada horitzontal. Bé, per decència, limitarem la mida de la matriu perquè el punt no vagi més enllà del camp.
Mireu, res de complicat. Però això no fa gaire perquè ha arribat el moment de dibuixar xifres. Treballarem de la manera següent: conservarem la referència al punt d’avituallament, que ja hem escrit, l’anomenarem punt principal o bloc principal. El bloc principal es mou en el sistema de coordenades de la matriu, ja ho hem fet. Totes les figures de Tetris consten de 4 blocs, és per això que, per cert, s’anomena Tetris.
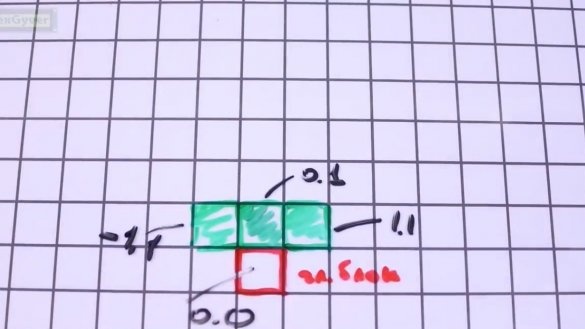
En conseqüència, ens queda acabar afegint 3 blocs més al bloc principal. Escrivim les seves coordenades al sistema de coordenades del bloc principal, de manera que el bloc principal estigui sempre per sota. És molt senzill, agafem la figura de la lletra invertida T. El bloc principal de baix a centre té coordenades 0.0 al seu sistema de coordenades.
El bloc superior és 0,1, el dret 1,1 i l'esquerra -1,1.
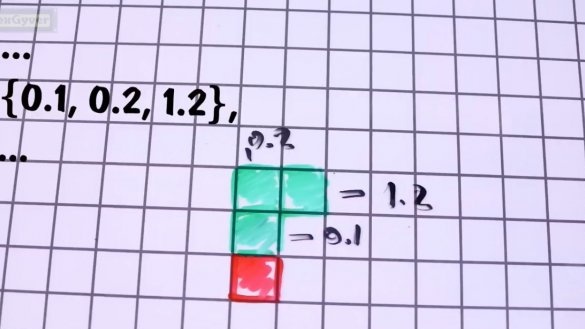
Agafeu la lletra G. El bloc inferior és 0,0, el següent 0,1, el següent 0,2 i la vora de la lletra 1.2.
Escrivim aquestes coordenades a la matriu en el següent formulari: {0.1, 0.2, 1.2} i deixem la matriu a la memòria flash per no malgastar la memòria dinàmica. Pel que fa a la rotació de les figures. És impossible rotar les figures. És divertit, és molt difícil explicar al microcontrolador com fer-ho. Per fer-ho, heu d’establir el centre de rotació, descomposar d’alguna manera la figura en parts i buscar noves coordenades per a cada part, tenint en compte una forta pixelació, que òbviament donarà lloc a errors i resultarà un disbarat. El problema es resol de manera senzilla, guardarem a la memòria les 4 posicions de totes les figures i totes.
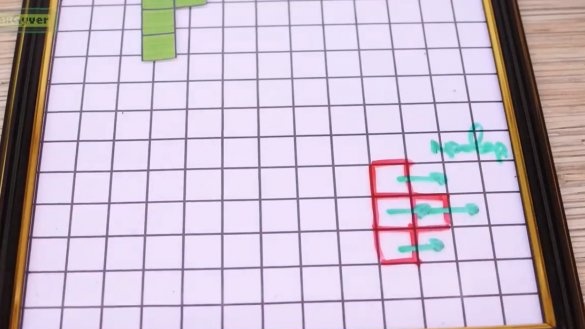
En realitat, ara queda seleccionar aleatòriament el número de la figura i dibuixar-la al voltant del bloc que cau. Aquí, per als tres blocs restants, agafem les coordenades de la memòria flash, les traduïm a les coordenades globals de la matriu i encenem els LED. Per cert, el color també s’escull a l’atzar entre els 6 colors més senzills i brillants de l’espai rgb. L’angle de gir de la figura al començament de la ronda també s’estableix de manera aleatòria i, quan premeu el botó cap amunt, només heu d’agafar el següent conjunt de coordenades per dibuixar-lo i girar-lo en sentit horari. Si es mou una forma, tot funciona igual. Primer, esborrem la figura a la posició anterior, és a dir, dibuixem-la de negre, després en la nova posició dibuixem el color actual de la figura. Al girar, de nou, esborrem la posició antiga i només en dibuixem una de nova.
Podeu descarregar el firmware a. Analitzarem només l’essència. Comencem comprovant les parets esquerra i dreta i la part inferior. Tot és molt senzill amb la part inferior, mirem a cada pas de la caiguda, la unitat base ha assolit una alçada de 0, això no és difícil, però cada vegada que premem el botó de control, hem de veure si el punt extrem de la forma de les parets laterals de la matriu tocava.
Si us toca, no moveu la figura. El mateix passa amb la rotació de les xifres. Per exemple, si la nova posició de la figura s’estén més enllà de les parets, la rotació està prohibida i, com que totes les formes que tenim són de diferents formes, els blocs extrems per a ells són diferents. Es podria pintar blocs extrems individuals per a cada figura per simplificar el treball del microcontrolador, però es pot considerar que ho van inventar.
Tot és molt senzill. Però la següent tasca és molt més interessant. Hem de revisar les col·lisions amb els blocs que ja hi ha a sotaSi tinguéssim una matriu que contingués l’estat de totes les cel·les del camp, seria més fàcil, però utilitzarem una matriu de colors per als píxels de la cinta, així tindrem la “màquina” més maca. Quin és el problema real. Tot sembla ser senzill, caure una figura verda i cada pas de la caiguda, cada canvi cap al costat i cada intent de girar han de comprovar si la figura de la nova posició es basa en les figures ja tombades. Si per a tots els blocs el color circumdant és igual al negre o igual al color de la figura, llavors permetrem el moviment en la direcció desitjada. Funcionarà fins que la forma de sota nostre sigui del mateix color que la que cau. En realitat és la "crossa": pintarem la forma caiguda amb un altre color. Torneu a pintar imperceptiblement els ulls, però es nota pel programa. Tot el que heu de fer és augmentar lleugerament la brillantor del color actual de la forma i tot això.
La figura va caure a la part inferior o una altra figura, la seva brillantor no va augmentar notablement, i a la nova ronda les figures que cauen deixaran de confondre el seu color amb les pròpies, cauran al damunt i igual de fixades, afegint lleugerament brillantor.
Per cert, quan premeu el botó cap avall, la figura es precipita a gran velocitat i pren el seu lloc.
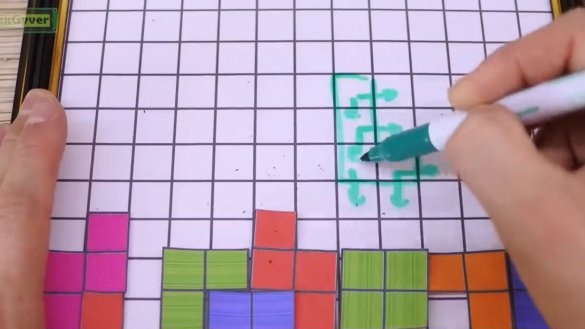
El nostre Tetris queda amb el toc final, és a dir, comprovar i netejar els nivells omplits horitzontalment. Tot és senzill aquí. Després de corregir la figura a la ronda actual, ens movem al llarg de les línies i comparem els colors dels píxels amb el negre. Si no hi ha un sol píxel negre a tota la línia, netejarem tota la línia.
Les línies detectades s’omplen de blanc, després la brillantor baixa gradualment a zero i s’obté l’animació. A més, tots els píxels, des de la primera línia d'ompliment fins a la part superior, es desplacen cap avall i el nombre de línies que s'han esborrat. Aquest procés es repeteix fins que no hi hagi nivells completats. També comprovem si hem arribat al cim, cosa que significa perdre. En aquest cas, es mostra un compte igual al nombre de nivells esborrats.
El compte es mostra en números, que es guarden a la memòria com a conjunt de zeros i zero, mitjançant els quals els LED s’encenen o s’apaguen. Això és el que sembla Tetris escrit a la matriu d’adreces. Gràcies per la vostra atenció. Ens veiem aviat!
Vídeo: